A Guide to Crosstabulations in Market Research
A complete guide to understanding the basics of crosstabs in market research. What do the terms mean? What do you need to understand?

Crosstabulations (often called tables or crosstabs) are the most common method of analysing market research survey data. This guide explains some of the most common elements of crosstabulations and some of the considerations you should make if you are new to crosstabulations.
A crosstabulation allows you to analyse one survey question (or variable) by another question (or variable). Even Microsoft Excel has a basic crosstabulation tool, although it refers to them as pivot tables, a term not used in market research circles. Below is a simple example of a crosstabulation:
From here, I will mostly refer to crosstabulations as tables
This table shows a cross-analysis of gender by age. The rows of the table are Male and Female, and the columns are three age categories. An alternative name for rows is stubs; alternative names for rows and columns are axes. Typically, a table contains a base row showing the number of respondents for each of the columns. A table also usually includes a total column showing the total respondents for each row.
The whole numbers in the table’s body show the number of respondents who fulfil both the row and column condition. These numbers (as opposed to the percentages) are usually referred to as counts, figures or absolutes. For example, of 831 respondents in the survey, 207 are Males aged 35-54. The percentages in the table are called column percentages (or vertical percentages). The most common percentages on a table are column percentages. In this table, 66% of the people aged 35-54 are Male. This percentage compares with 58% of all the respondents in the survey overall that are Male.
Column percentages allow you to compare the percentage of respondents in each row for different categories in the table columns. In this example, you can see a greater proportion of Females (53%) for the age group 55+ than the other age groups. Although there are fewer Females aged 55+ (118 respondents) than Females 16-34 (128 respondents), the percentage of Female respondents in each category is greater for respondents who are 55+.
The table also contains texts to identify the table and explain its contents. It is common practice to show a project title (National Cycling Survey), a table ID (Table 1), a table title (Gender by Age), and a base title (All respondents).
For most surveys, it is common practice to analyse each question by several other questions. In Table 2, you will see that the analysis shows Question 1 by both Gender and Age. Gender and Age are referred to as banners; effectively, they are the columns of the table. They are also commonly referred to as table banners, breaks, breakdowns, headings or columns. Most surveys will have a standard banner in use, including important demographics, such as gender, age and region.
Additionally, researchers will often include other key differentiators in a banner, such as buyers/non-buyers. A banner is then typically used for initial analysis for all or most questions. The example in Table 2 only has two demographic questions in its banner; there are usually more categories.
The table also has a Not answered category at the bottom of the table so that the rows of the table add to 100%. The Not answered category clarifies that one respondent refused or was unable to answer this question. Some researchers prefer to remove this respondent from the table so that the table only includes 830 respondents. However, being aware of the level of not answering can be important information. If, for example, 30% of respondents did not know whether they owned a bicycle, this would be important, if somewhat curious, information.
You may note that the percentage for Not answered in two columns is *%. This notation is a common way of denoting that the figure is greater than 0% but less than 0.5%. As a small percentage might round down to 0%, an alternative approach is to show one decimal place for percentages to differentiate between 0% and 0.1%, for example.
The title for the table is Q1 Whether own a bicycle. It is common practice to change table titles to statements rather than the actual question asked in the questionnaire. In this case, the table has a title of Q1 Whether own a bicycle. You could also have ‘Bicycle ownership’ instead of the wording on the questionnaire, which was ‘Do you own a bicycle?’. The main reason for this is that some questions may have long texts or explanations, which will be difficult to read quickly on a table.
The questions we have looked at so far (Gender, Age, Bicycle Ownership) can only have one answer – or no answer if the respondent refuses to answer or does not know. For some questions, any number of responses are possible. These are often referred to as multiple-response questions.
In Table 3, respondents indicate which makes of bicycle that they like. In other words, they could choose none, one, two, three or all four makes. Of course, if they select None of these, they cannot pick any of the makes of bicycle. This table’s rows could add up to anything from 100% to 400%, depending on the number of answers given. Although we can see that 40% of Males like Fastwheels and 39% of Males like Two-wheelz, we do not know whether these are predominantly the same people or different people. We look at this in a bit more depth later.
Table 4 shows the same data as Table 3, with the percentages calculated horizontally. This table shows what is usually referred to as row percentages or horizontal percentages. In other words, this table shows that almost two-thirds of the people that choose Two-wheelz were Male. However, it is important to consider that there are over 100 more Males in the sample than Females. This data contrasts with Fastwheels, where there is an almost even split between Males and Females even though there are far more Males in the sample. This data needs careful interpretation.
Sometimes, column percentages and row percentages appear on the same table. While this can be confusing initially, the percentages with no data in the total column will be row percentages. The percentages with no data in the total row will be the column percentages unless the tabulation software programme outputs 100% on the total rows and columns.
While column percentages with each row based on the total row are the most common way of displaying tabulated data from response questions, it is sometimes beneficial to show cumulative column percentages. In Table 5, there is a table showing the last occasion that respondents rode their bicycle. The figures in this table add to 100%.
Table 6 (below) shows the cumulative figures and percentages such that the row Within the last fortnight includes respondents in the Within the last week row added to the Within the last fortnight row. The third row includes everyone in the first three responses, and so on. Finally, the Longer ago row only includes respondents who answered longer ago than one year. Where cumulative percentages are in use, it is important to indicate this on the table to reduce the risk of misinterpretation.
Less frequently, every table cell is based on the total respondents, as in Table 7. In other words, the 94 Males who rode their bicycle within the last week is not based on the 479 Males to provide a column percentage but is based on 831 respondents. This calculation is usually referred to as total percentages or percentages based on total. In this case, the body of the table – all table cells except those in the total row and total column, add to 100%. It is sometimes called sample profiling.
When producing crosstabulations, there is often a need to provide sub-totals, also referred to as nets.
In Table 8, there is a sub-total for 35+. This row is generated by adding together the two age groups 35-54 and 55+. One reason for producing sub-totals is that percentages are usually rounded to the nearest whole number. Looking at the total column for this table, by adding 35-54 (38%) to 55+ (27%), you might mistakenly calculate 35+ as 65% when, in fact, it is 64%. Most market research software rounds percentages up to the nearest whole number so that 40.5% would display as 41%.
Sometimes, it makes sense to show percentages to one or two decimal places. Showing decimal places does not change the effects of rounding as it will take place on the next significant digit. However, discrepancies caused by rounding become less sensitive when an additional decimal place is available, as in Table 9.
In the example now, looking at the total column, it is clear that 35-54 (37.7%) and 55+ (26.7%) give a sub-total of 64.4% for 35+. However, if rounding took place at the second decimal place, there might be a difference between the sum of the percentage and the correct percentage.
As already mentioned briefly, multiple response questions are more difficult to interpret, as each respondent may fit into any number of categories. There are some useful techniques to make it easier to work with multiple-response questions. In Table 10, there is a count of responses at the bottom of the table. Unfortunately, there is no real standard name for this type of data.
The count of responses is the sum of the answers in the rows. In Table 10, you can see that the total responses are 969 from 831 respondents. The percentage of 117% indicates that there is an average of 1.17 responses per respondent. However, this table includes a row, No bicycle owned, which, by definition, must mean that a respondent is not also present for any of the makes of bicycle.
One solution to this is to exclude anyone saying No bicycle owned from the table. Table 11 shows that the number of respondents in the table has reduced from 831 in Table 10 to 755. The table is effectively excluding the 76 respondents who indicated No bicycle owned in Table 10. The figures in Table 11 remained unchanged (excluding the removal of ‘No bicycle owned’), but the percentages are now higher as they are percentaged on 755 respondents instead of 831.
Another technique that you may need is to produce market share data or share of responses.
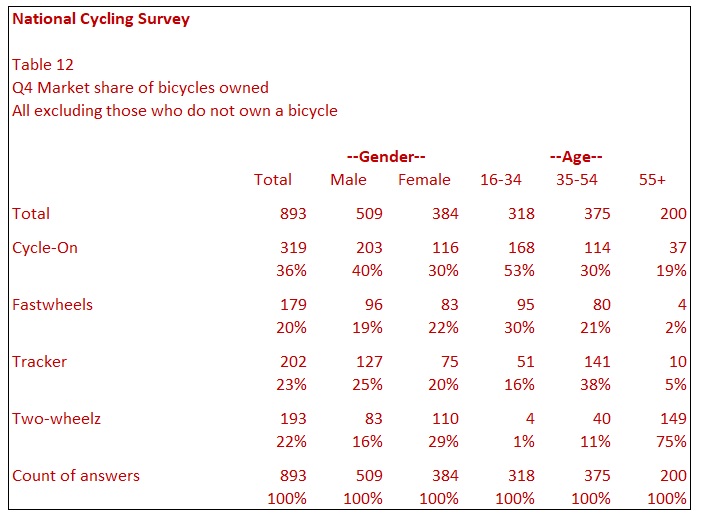
Table 12 is the same as Table 11, except the total row is the sum of the responses for each of the four makes of bicycle. By adding the rows together (or generating a total row of total responses), the table will now add to 100% and give you the percentage of market share data. When producing tables like this, it is important to clarify what the data means with clear labelling and titling
So far, this guide has only covered questions where there is a list of responses. Some questions contain a numeric value – for example, the number of children, the distance travelled, the number of packs of a product bought etc. There are various ways that numeric data can appear in crosstabulation; we will explore these now.
One way of understanding the data from a numeric data question is to display all the responses as rows of a table.
In such cases, it is normal to show all the values in ascending order, although, in some cases, it may be more appropriate to display answers in descending order. This approach works quite well to see the range of responses and whether there are any outliers. This type of table has no common terminology associated with it – value distribution table is, perhaps, the most common term. When producing a value distribution table, it is normal to have a mean score at the bottom of the table. The mean score is the sum of the values given by each respondent, divided by the number of respondents. There is a section that covers mean scores and other statistics later in this guide.
It is always worth remembering that a mean score can be skewed by a small number of exceptionally high or low values. Table 13 shows that the mean score for the data in the main part of the table is 5.0, although it is much higher (6.5) for those aged 16-34. Again, you need to apply care when interpreting this data as a small base will make the mean score more volatile to a small number of outlying values. Statistical tests are used to explain the significance of these differences (see the section covering statistics and significance tests).
Table 13 is difficult to understand quickly if you want split cyclists who ride into, say, low, medium and high bands. The usual solution is to break values from a numeric question into ranges.
Table 14 shows the same data as Table 13 but has placed respondents into five bands. The data is instantly more readable. It is important to take care not to choose bands that may distort the interpretation of the data. For example, if most of the respondents in the 3 to 5 Km category only cycled 3 Km, the results may give a different impression if the bands were Up to 3 Km, 4 to 5 Km etc. However, this table offers the benefit of seeing why those aged 16-34 have a higher mean score. Again, it makes sense to show the mean score on this table. It is better to display the actual mean score rather than use midpoints for the ranges. You could score 3 to 5 Km as 4 Km, but this might distort the mean score. Using the actual value of 3, 4 or 5 Km for this calculation is far better.
‘Variables’ is a term that has subtly different meanings in market research. Many people refer to variables as data combined from one or more questions. Examples are:
Other people refer to any data construct as a variable. Therefore, a question on the questionnaire is a variable as it stands. For example, the Yes and No responses in Q1 (Table 2) form a variable.
There are several statistical tests that most tabulation software programs will have as standard features.
Table 15 shows the same table as Table 14 but with some of the most common table-based statistical options. To take each in turn:
Median – this is the ‘middle’ value. In other words, as there are 831 respondents in the table, the median will be the value of the 416th value if the values are in sequential order. The median for Males is 3. The median means that 415 respondents had a value of 3 or less, and 415 respondents had a value of 3 or more.
Maximum – this shows the maximum value found among any of the respondents in each column. For example, the highest value amongst Males is 64, whereas it is 84 for Females. (Minimum can also be displayed, showing the lowest value for each column).
Mode – The mode is often confused with the median. The mode is the most common value for each column. For Females, the most common value is 2, whereas it is 3 for Males. The N/A value for those aged 16-34 indicates that two or more values appear most frequently. Table 13 shows that the values of 2 and 3 have the same number of respondents for those aged 16-34.
Mean score – This is the most common table-based statistic. It is the sum of the scores divided by the number of people giving that score. For example, scores of 1, 3, 3 and 9 would sum to 16 from 4 respondents, meaning that the mean score is 16 divided by 4, which equals 4.
Standard Deviation – The standard deviation is a statistical calculation that measures how far the values vary from the mean. The higher the value, the more dispersed the values are in relation to the mean.
Standard Error – The standard error uses the standard deviation to calculate the reliability of a mean. A low value (close to zero) indicates high reliability. A lower value is usually associated with larger sample sizes.
Other statistical tests – There are several other table-based statistical tests, including Error Variance, Kolmogorov Smirnoff Test, and various forms of significance tests. Significance tests and their interpretation are covered separately in this guide. There are also multivariate statistical tests that are not relevant to crosstabulations except where their output is used as variables for analysis purposes, such as clusters from cluster analysis.
When analysing multi-response questions in crosstabulations, it is sometimes desirable to see the overlap of answers.
Table 16 shows a cross-analysis of Q4 by itself. You will see that there is a diagonal line of 100% values. This table also gives some indication of what answers cluster together. For example, in the table’s Tracker column, you can see that 22% of the Tracker owners also own a Fastwheels bicycle. This information contrasts with the Two-Wheelz row in the same column where only 5% of Tracker owners also own a Two-Wheelz bicycle. You might put this difference down to fewer people owning a Two-Wheelz bicycle, but, in fact, more people own a Two-Wheelz bicycle than a Fastwheels bicycle.
There are many times when you do not want to see the data in a table for all respondents. Sometimes, this is due to the nature of the question on the questionnaire. For example, you may have a question which asks ‘Have you heard of Product X’ and a second question which asks ‘How long ago did you first hear about Product X’. In such a case, you would typically only want respondents who have heard of Product X at the first question to appear in the table for the second question.
This technique is known as applying a base to a table or applying a table filter. It is also sometimes referred to as data filtering, although data filtering strictly refers to including and excluding data from questions or variables rather than the tables themselves.
Sometimes, a base or filter is applied to a table to look in more depth at a particular sub-sample. For example, you could produce any of the tables shown already but based on those living in the ‘North’ region, for example. This type of filter works in the same way. Still, it is slightly different from the first example, where a logical filter was applied to a table because only certain respondents answered another question. In this case, the table is being filtered on a sub-sample of respondents.
Earlier in this guide, Table 12 had a filter. The table only included those respondents who own any of the four makes of bicycle – or, to put it another way, excluded those that answered ‘none of these’.
When applying a base or filter, it is important to label the table to clarify that data has been filtered on certain respondents only. As a result of the filter, the table figures will be percentaged on the filtered base row. Table 12 shows a table with a filter.
When applying filters to tables, it is important to be careful when working with small samples. If the total base for a table is, say, ten respondents, the percentages in the table are highly volatile. Each respondent effectively accounts for 10%. For this reason, it is good practice to show the base row so that those inspecting the table can see where the data may be unreliable. This issue can be particularly problematic if you share data with clients for interactive analysis. If the tabulation software or dashboard does not show the base and does not show the figures, it is easy to place too much trust in percentages on their own. It is good practice to suppress columns, row or entire tables if bases are low in some cases.
Many questionnaires have rating scale questions where respondents have a (usually) balanced range of responses they can choose. For example, a rating question may have responses of very good, quite good, neither good nor poor, quite poor and very poor. These questions often appear as a grid question with a battery of rating scale questions or statements. For example, when surveying customers of a fast-food outlet, you may ask about the overall service, the product, the price, the cleanliness of the outlet etc., using the same responses for each rating.
Table 17 is a table which is showing the analysis from a single rating scale question. The table looks like other tables already covered with one minor difference. You will note that each row has a value in brackets except for the ‘Not sure‘ row. The values in brackets indicate the score that is being applied to each row. For example, respondents choosing Very good get a score of 2, respondents choosing Quite good a score of 1 etc. This scoring system means that it is possible to produce a mean score showing the average rating. Males show a mean score of 0.74, while Females have a slightly lower score of 0.69. The average rating is, therefore, above the midpoint but not as high as quite good. The mean score makes it easy to compare means across different banner categories. You will note that ‘Not sure’ has no score and is excluded from the mean score calculation.
One consideration when looking at mean scores is that it does not indicate the spread of answers. For example, if 50% of the sample chose ‘Very good’ and 50% ‘Very poor’, a mean score of 0.0 would result. However, if everyone (100%) chose the midpoint ‘Neither good nor poor’, that would also return a result of 0.0. For this reason, it is useful to show the standard deviation to give a statistical indication of the spread of answers.
It is common for rating scale questions to show the top two boxes and bottom two boxes.
Table 18 shows the top and bottom two boxes. The term ‘top two boxes’ means those answering either of the top two answers – Very good or Quite good. Similarly, ‘the bottom two boxes’ means those answering either of the two bottom answers – Very poor or Quite poor. Of course, you can apply the summing of the higher and lower ratings for any rating scale. For example, if you have a seven-point rating scale, you might show the top three and bottom three options. There is only a reference to the top two and bottom boxes in this guide as it is the most common grouping.
Another common rating system, which is particularly common on customer feedback surveys, is the Net Promoter Score. Net Promoter Score is often applied on a rating scale of 0 to 10, where a respondent is typically rating the quality of service. The Net Promoter Score works as follows:
Net Promoter Score = Promoters minus Detractors.
Again, when using this commonly used calculation, you need to handle it with care. See the notes above on ‘interpretation of mean score data’.
Many questionnaires have rating scale grids where a series of statements or questions use the same responses. Often, a table for each statement appears in a volume of tables. These can be slow to interpret. Therefore, it is normal to summarise such tables.
Table 19 is one type of summary table. Such a table is sometimes referred to as a banked table. The table is effectively the total columns of the data for each make of bicycle shown in one table. You will note that the base for each column is the same (831). This table makes a comparison of each make of bicycle easy. You can see that New Two-Wheelz scores more highly than the other makes. In this table, though, you lose some granularity. You cannot, for example, compare males with females. You could produce two tables filtered on gender – one for males and one for females.
Table 20 provides an even more condensed summary of the data, but this time you can compare Gender and Age easily. The table shows the mean scores for each make as the rows. You can see, for example, that the make, Tracker, scores far higher amongst the older age groups.
Another way of summarising data from rating scales is to show the top two boxes data for each statement. Table 21 shows that those rating each make as being very likely or quite likely to purchase. Again, this table can show data for Gender and Age.
For some tables, particularly where there is a long list of responses, it may be easier to use data with the rows ranked in descending order. In other words, the row with the highest figure appears at the top of the table, and the row with the lowest figure appears at the bottom.
Table 22 shows Q2 in rank order. Fastwheels appears at the top of the table as more respondents choose this make than others. Two-wheelz appears second as it is the second-highest and so on. It is good practice to leave rows such as ‘None of these’ or ‘Other’ at the bottom of the table.
Sometimes there are two o more levels of data in the table’s rows. In such cases, it may make sense to use a two-level ranking. One example of this is where you are showing the makes and models of cars. Each model is a sub-category of a particular make. It may make sense to rank the table on makes and then the models within that make.
In Table 23, responses have been grouped into sub-total (nets), showing answers related to bicycle maintenance and bicycle usage. The answers Mending your bicycle, Tyres that are best value and The cost of bicycle repairs comprise the net called Bicycle Maintenance. Similarly, three rows comprise Bicycle Usage.
Table 24 shows the same data but with the rows ranked. Firstly, ranking is applied to the two nets and then answers comprising each net appear in the following rows. In Table 24, Bicycle Usage moves to the top of the table. The categories within Bicycle Usage are also ranked. This means that Exercise on Bicycle appears as the next row under its net. Following this comes Holidaying and Cycle racing. The responses for Bicycle Maintenance are also sorted into rank order, while None of these is anchored at the bottom.
One of the few weaknesses of crosstabulations is that it is difficult or impossible to see the combination of answers.
In Table 25, there is a table that shows whether respondents have ever owned a car or motorcycle. The table does not show how many respondents:
That is four combinations of possible answers from two responses in the questionnaire. If there were three more possible answers on the questionnaires, the number of combinations would increase. In such cases, multivariate analysis can cluster respondents together. However, most tabulation software does not have multivariate analysis tools.
In Table 26, we get a much clearer picture of the story behind the data. It is now easy to see that older respondents are more likely to have owned both a car and a motorbike. Younger respondents are more likely to have only owned a motorbike. There are no major differences between gender. There were clues to this information in Table 25, but Table 26 makes it easier to understand the underlying data.
Most tables have a table banner, although, of course, you can produce a table with a total column only. It is common practice to use a standard banner to analyse the data from every question. This approach is a good starting point to understand the data; more in-depth analysis can follow later. Deciding what appears in a banner can be a difficult choice. Having too many categories in the banner may make it too difficult to view results easily, whereas having too few may mean missing some important differences between groups.
Most of the tables shown so far only have Gender and Age as banners. This is not typical and has largely been limited to Gender and Age so that the table fits easily within this document. Typically, banners should contain the main demographic questions such as Age, Gender, Region, Income level, Presence of children etc. Other factors may be of primary importance in some markets, such as ethnicity. It may make sense to include other key non-demographic questions – for example, buyer/non-buyers, in-store customers/online customers etc. The non-demographic questions are more likely to be dependent on the subject matter of the survey.
Some tabulation software may have a limitation on the number of banner points that you can have. This limitation may vary from as few as 20 categories up to thousands of columns of data. It is important to avoid choosing banner points that may have small bases. If bases are small, certainly less than 30, it is important to remember that each respondent’s answer may have a noticeable effect on the percentages reported. For example, if a base is 25, one respondent will count as 4%.
Nested variables mean that you can show demographic questions within each other. This analysis can provide interesting insights. Table 27 shows each category within the two genders. For example, the percentages across Gender and Age for the row ‘Car’ are similar in Table 25. Yet, when we see Table 27, we can see big differences between Males 16-34 and Females 16-34.
Weighting is often used in market research to adjust a sample to represent the desired sample (usually called target weighting). For example, you may collect data from 60 males and 40 males, yet your desired target is a 50-50 split of males/females. To weight the data collected to the desired targets, you would give each male a value of 50/60 (approximately 0.83) and each female a value of 50/40 (1.25). The values of 0.83 and 1.25 are known as weighting factors. This means that rather than each female in your sample containing as 1, a female would count as 1.25. There are four types of weighting as follows:
Target weighting is as described in the previous paragraph. However, it can be more complex than the example given. You may wish to set targets for each of three age groups within two genders – in other words, for six cells. Let’s say you want the following targets:
Males 16-34 – 20%, Males 35-54 – 20%, Males 55+ – 10%
Females 16-34 – 20%, Females 35-54 – 20%, Males 55+ – 10%
You will note that the targets add to 100%. Targets will add to 100% if they are in terms of percentages, but they may in terms of figures. This approach is known as rebalancing the sample. It means that you are adjusting the proportion of respondents for Age within Gender. Sometimes weighting is to, for example, match a population or customer profile. For example, you might weight Males 16-34 to 5.7 million if there are that number of males 16-34 in a particular country. Males 35-54 might be weighted to 6.2 million and so on.
Table 1 above is a repeat of the table shown earlier in this guide. The cells marked in green are the sample sizes for the six cells that form the target weighting matrix. What this table shows is the actual sample size we have. For example, there are 168 Males aged 16-34. If we divide 168 by 831 (the total sample), we will find that Males aged 16-34 are 20.22% of the sample. To adjust males to be exactly 20%, we will need to weight Males 16-34 by 20 / 20.22, which produces a weighting factor of 0.989. This needs to be repeated for the other five cells. Most tabulation software packages have a facility to calculate this automatically for you. The weighting factors when calculated are:
Males 16-34 – 0.989, Males 35-54 – 0.803, Males 55+ – 0.799
Females 16-34 – 1.298, Females 35-54 – 1.568 – 20%, Females 55+ – 0.704
You will note that the range of weights is 0.704 to 1.568; females 35-54 were, therefore, the most under-represented in our sample data.
Once the weighting is applied, it is easy to check that it has worked correctly. Table 28 shows that the percentages for Males and Females in each group are 50%. This is because the sum of Males 16-34, Males 35-54 and Males 55+ added to 50% and likewise for Females.
By a similar summation, we can see that the percentage for each age group under the Male and Female columns is 40%, 40% and 20%, respectively. This matches the targets set of Males 16-34 (20%) and Females 16-34 (20%), giving a total of 40%.
You will note that both Table 28 and Table 29 have an Unweighted Row; this is the sample size for each column before weighting, i.e. the actual number of respondents in the sample. Generally accepted market research standards dictate that unweighted total rows should always be present on all tables when there is target weighting.
More complex target weighting matrices
The examples so far have discussed weighting to one demographic (Gender) and two demographics (Age within Gender). Of course, it is possible to have target weighting to three or more variables or demographics (e.g. Age within Gender within Region). Generally, the more cells you have, the bigger the sample you will need to weight the data reliably. See notes on good practice in weighting later.
Rim weighting is similar to the previous example but is a special form of target weighting. In the target weighting example, I set targets for each Age group within Gender. Rim weighting allows you to set separate targets for Gender and Age. This type of weighting is often necessary where data for the interlocking cells is not available; in other words, you do not have targets for Males 16-34, Males 35-54 etc.
For example, your targets might be:
Males – 60%, Females – 40%
16-34 – 50%, 35-54 – 30%, 55+ – 20%
In this case, each demographic has a total target of 100%.
Rim weighting uses an arithmetic algorithm to adjust the samples for the targets. The algorithm calculates weights for the first target (Gender, in this case) and then applies a multiplicative weight to adjust for the Age targets. It repeats this process (called iterations) until the arithmetic algorithm converges on the desired targets. This topic is discussed in more detail here.
Table 30 shows the effect of the rim weighting described above. We can see that the split for Males and Females is 60/40%.
Table 31 similarly shows the effect of the rim weighting for the Age question.
Once again, the unweighted row shows the actual number of respondents in each column of the table.
Factor weighting is much simpler to understand. Factor weighting means that the weights are part of the data. This scenario may occur when the data has already been processed and passed on or imported from another system. For the tables, the weight would be applied as described before without any calculations. As before, unweighted rows should be shown.
Volumetrics (often called quantity weighting) is entirely different from the other weighting types and bears little resemblance to other weighting. In the three examples – target weighting, rim weighting, factor weighting – a weighting value is applied to each respondent’s data. Volumetrics are tables that are scaled by a value within the data (not factor weights). For example, you may wish to produce a table based on the number of cans of a soft drink consumed. The table would no longer be showing data in terms of respondents but in terms of cans consumed. A respondent drinking three cans would count three times, while a respondent drinking five cans would count five times. In such cases, there is no need to show an unweighted total row (there is no respondent weighting), but clear labelling should indicate that the table is displaying data in terms of cans. The total row using this example would be the total number of cans consumed for each column of data.
When weighting data, it is important to check that there are no empty cells in the weighting matrix. For example, if the sample had no Females 55+, you cannot weight zero respondents to a target (unless it is also zero). This potential problem becomes a risk if you have a big matrix or rim weighting with too many cells. It is important to check for empty cells before trying to apply target weighting.
A similar problem to having empty cells is the risk of cells with small bases. If you have a sample size of 200 and your weighting matrix has 40 cells, there is a high chance that some cells may only have 1 or 2 respondents. A good way to check that weights do not have too much influence is to check the effective sample size (see the next topic) and check the range of weighting factors. Although statisticians do not always agree, many believe that the range of weights should fall between 0.5 and 2.0 in most cases.
Most good tabulation software programs will allow you to produce the effective sample size. This figure is a statistical calculation that shows the equivalent sample size you could have had to achieve the same accuracy of data without weighting if your sampling had been correct. The effective sample size will always be less than the actual sample size when weighting is applied (excluding volumetrics). If you had a sample of 1000 and the effective sample size is 800, you could have achieved the same statistical accuracy level by correctly sampling 800 respondents. In other words, there were potentially 200 wasted interviews.
Table 32 shows the same data as Table 31 with the effective sample size shown. It is good practice to show the effective sample size if the software you are using allows this. Table 32 indicates that the Effective Sample is 760. Researchers sometimes refer to this as weighting efficiency of 91.46%, which is 760 as a percentage of 831.
One of the most commonly used tests to detect important differences in tabulations is a significance test. In simple terms, the purpose of a significance test is to show whether differences between two data points are significant enough to be ‘real’ rather than by chance. A significance test compares the figures in each row of a table. When applying a significance test, you always use a confidence limit (or limits). You are effectively saying, for example, that with 90% confidence, one data value is significantly different from another data value.
In Table 33, a previously used table now has the significance tests showing. Values that are significantly different have letters to indicate their difference. Each column in the table has a letter assigned to it as indicated in the texts. Male is a, Female is b, 16-34 is c etc. The value of 183 (52%) for females in the row for Fastwheels has A underneath it. The ‘A’ refers to the fact that the figure of 183 (52%) is significantly different (and greater) than the figure of 190 (40%) in the Male column. In this table, a lower case ‘a’ indicates that the figure is significantly different with 90% confidence and an upper case ‘A’ indicates that this figure is significantly different with 95% confidence. You will note that there is a footnote at the bottom of the file to explain this. The lower case ‘cd’ for Fastwheels in the 55+ column indicates a lower confidence level of 90%.
Although some tabulation software presents data slightly differently, some general standards are widely in place:
Researchers use both T-Tests and Z-Tests to calculate significant differences. Most tabulation software will use one or the other, although some allow for both. In samples over 100, T-Tests and Z-Tests will show very similar results. Generally, it is not good practice to run significance tests on small samples – for example, if there are less than 30 people in a table column. Many software products ‘hide’ significant differences in small samples, but this will vary from product to product. Further, the person using the tables to interpret the data should be proficient in understanding this vulnerability.
The example shown is the most common example used. There are, however, several common variants and other uses of significant tests. Examples are as follows:
Like some other types of market research software, tabulation software breaks down into two main types. These are:
Some menu-driven software products also support a scripting language. In most cases, this is using an external programming language, such as Python, JavaScript or R.
Our MRDCL tabulation software is a scripting language. It uses the same engine as QPSMR, which is a menu-driven product. It means you can transfer a project from QPSMR to MRDCL in seconds (or vice versa). MRDCL uses its own scripting language, which has been developed specifically for the market research industry. There has never been a need for an external programming language, such as Python, as MRDCL is a complete system handling any crosstabulation needs. This approach maximises productivity.
This topic is discussed more fully in a blog article.
The best tabulation software or combination of software products is where you have enough flexibility to meet each project’s and each client’s demands. This message may not be true where you are only handling simple projects, or every project has very similar requirements. The reason for the need for flexibility is mainly due to the changing demands of market research.
The path of a market research project has changed and continues to change. Sometimes, tabulations are the final output from which a client or researcher may prepare a report – or, in some cases, interpret and use the data directly. But, there are many other scenarios. For example:
In all these scenarios (and more), MRDCL delivers tools that handle these needs cost-effectively. MRDCL links to Resolve, a free product that allows clients and colleagues to analyse projects prepared in MRDCL (or QPSMR). Most products do not offer this flexibility.
As data increases globally, the expectation is that you can transfer data from one system to another easily. Some of the
things that we have improved significantly in our MRDCL software are:
MRDCL continues to develop in these key areas and always welcomes feedback and ideas on how to improve.
Absolutes – The number of respondents in each cell of a table. They are often referred to as figures.
Axes – The questions or variables used as the rows and columns of a table
Banked Table – Typically, a summary table (like Table 19) that has data from two or more questions or variables “banked” side by side or one under the other
Banners – The columns of a table, either referring to the group of individual columns or the questions and variables used for the columns.
Base Row – Usually, the first row of a table that shows the number of respondents included in the table for each column. Sometimes, this row appears at the bottom.
Base Title – Text that usually appears at the top of a table to indicate the respondents included in the table.
Bottom Two Boxes – See top two boxes
Breakdowns – The columns you used to analyse the data in the table (see banners)
Breaks – See breakdowns
Column Percentages – Percentages in a table calculated by dividing the figure in a cell by the figure in the base row for the same column.
Columns – The categories that appear horizontally on a table. See banners.
Count of Responses -The number of responses that either a respondent gives or the respondents in a table give in total.
Crosstabs – See crosstabulations.
Crosstabulations – The matrix of figures where one or more questions or variables are analysed by one or more questions or variables.
Cumulative Percentages – Percentages where each second and subsequent row or column is the sum of the current row or column and all previous rows or columns.
Effective Sample Size – A statistical calculation that shows the equivalent sample size you could have had to achieve the same accuracy of data without weighting if your sampling had been correct.
Factor Weighting – The application of a weight to individual respondents or specific respondents.
Figures – The number of respondents in the cell of a table.
Filter – See filter on sub-samples and logical filter.
Filter on Sub-samples – The selection of a group or type of respondents included in a table.
Grid Question – A series of statements, rating or list of items (such as brands) with the same possible responses.
Headings – Sometimes used to refer to a table’s titling to indicate a table’s content; sometimes used to refer to the columns or banners.
Horizontal Percentages – Percentages in a table calculated by dividing the figure in a cell by the figure in the base column for the same row.
Logical Filter – The respondents that logically answer a question, thus removing those respondents who do not answer a question.
Market Share Data – A table that shows the percentage of answers (typically, brands) given as a percentage of the sum of the answers.
Maximum – The highest value from any of the respondents in the column of a table.
Mean score – The average value, calculated by dividing the sum of the scores by the number of respondents answering.
Median – The middle value from all the answers provided by a group of respondents.
Minimum – The lowest value from any of the respondents in a column of a table.
Missing data/empty cells – A problem encountered in weighting procedures where there are no respondents in a weighting matrix cell. Also, it refers to any missing data where a question is unanswered.
Mode – The most frequent value in a column of a table.
Multiple-response questions – Questions where respondents may give more than one response.
Multivariate Statistical Tests – A series of statistical tests that analyse the influence of multiple questions or variables.
Nested variables – This refers to a variable constructed by showing the different combination of responses within two or more variables, e.g. for age with gender, a nested variable might contain Males 16-34, Males 35-54, Males 55+, Females 16-34, Females 35-54, Females 55+.
Net Promoter Score – This is a commonly used calculation used in customer feedback surveys. Using a scale from 0 to 10, the percentage of detractors (scores 0 to 6) is subtracted from the percentage of promoters (scores 9 or 10) to give the net promoter score.
Nets – Nets calculate the number of respondents who answer choose from any answer from two or more responses. If a respondent chooses two or more responses, they would only count once.
Numeric data – These are questions or variables that contain a value; this may be a whole number of a number with decimal places.
Ranking tables – When a table is ranked, the rows are shown in descending order. The order of the responses is usually taken from the total column, but another column can be used. Sometimes, table columns are also shown in rank order, but this is less common.
Rating Scale Grids – See grid questions.
Rim Weighting – This type of weighting scales respondents to two or more independent targets. For example, there are separate targets for gender, age and region.
Row Percentages – See horizontal percentages.
Rows – These are the responses that appear down the left-hand side of a crosstabulation.
Significance Tests – The purpose of a significance test is to show whether differences between two data points are significant enough to be ‘real’ rather than by chance
Standard Deviation – The standard deviation is a statistical calculation that measures how far the values vary from the mean.
Standard Error – The standard error uses the standard deviation to calculate the reliability of a mean.
Statistical Tests – Several statistical tests can be used on tables. The most commonly used ones are mean score, standard deviation, standard error, error variance, T-Tests, Z-Tests, significance tests.
Stubs – This term is used sometimes to mean the rows of a table.
Sub-totals – See nets.
Summary Table – A table that summarises data from two or more questions or variables.
Table Cell – This refers to a single data point in a table. For example, if you analyse gender (as rows) by three age groups (as columns), one of the cells in the middle of the table would contain data for males aged 35-44.
Table ID – This is a unique number or name that is allocated to a specific table.
Table Title – This is a title, usually at the top of the table, which explains the contents of the table
Tables – A term used instead of crosstabulations and crosstabs.
Target Weighting – This is the process of scaling respondents to meet the desired population or ratios.
Top Two Boxes – This term describes respondents who give either of the two most positive ratings in a 5-point rating scale, e.g. very good or quite good. The bottom two box is also commonly used, indicating those choosing the two most negative ratings of a 5-point scale. The top three and bottom three boxes are also used in 7-point scales.
Total Base – See base row.
Total Column – Usually, the first column of a table that shows the number of respondents included in the table for each row. Sometimes, this column appears at the right.
Total Percentages – This is where every figure in the table in percentaged on everyone included in the table (i.e. those fulfilling the filter). It is uncommon to use this type of percentage.
Unweighted Total Row – When target or rim weighting is in use, it is strongly recommended that an unweighted total row is used to show the actual number of respondents in each column before weighting has been applied.
Value Distribution Table – This type of table gives a count of all the values found in a numeric question or variable. The table is typically shown in ascending order of values with a mean score at the bottom of the table.
Variable – The term is in use interchangeably. In some cases, a variable refers to data generated from one or more questions, i.e. displaying data differently from the original questions on a questionnaire. Others, however, call this a derived variable and refer to all questions and derived variables as variables.
Vertical Percentages – See column percentages.
Volumetrics – These are tables where the data is not in terms of respondents but in terms of some other quantity, e.g. money spent, cans consumed.
Weighting – See target weighting
Weighting Factor – This is the actual value applied to an individual respondent after performing target weighting or rim weighting.
I have worked with crosstabulations for over 40 years. I have been lucky enough to work on some of the most complex data and tabulation requirements over my time. I started by learning how to produce tabulations from software products that are mostly long forgotten, such as XTAB7, Sage and Quantum.
For ma
I put together this guide to cover the most common considerations when analysing survey data and showing results as crosstabulations. I have certainly not covered some of the most complex data or tabulations that I have ever worked on, but this guide should give you a good grounding for market research tabulations.
Of course, nothing is perfect, so if you can think of a way to improve this guide, please drop me an email at phil.hearn@mrdcsoftware.com. Similarly, if you want any help or advice, I will do my best to help you.
Phil Hearn
March 2021